非对称加密算法
原理
对称加密算法
在了解非对称加密算法之前,我们先看一下对称加密算法。对称加密算法就是传统的用一个密码来对文件、文档进行加密和解密的算法。也就是说,通过这个密钥,我们可以把数据加密,当我们需要使用这个数据,从而对其进行解密的时候,我们使用的解密的密钥同加密的密钥一样。加密和解密的密钥相同,我们称之为对称加密算法。从程序上看,它就是一个接受message和key的函数,然后输出的是加密后的密文。
1 | secret = encrypt(Key,message); |
而解密则相反,它接收密码和密文,然后输出我们需要的明文。
1 | plain = decrypt(Key,secret); |
现在常用的对称加密算法有:
- DES:密钥长度 56/64
- AES:密钥长度 128/192/256
- IDEA:密钥长度 128
我们可以很容易的知道,加密强度和我们的密钥长度成正比。
然而,在我们平时的生活中,我们其实输入的密码的位数只有几位~十几位不等。远远没有达到这些对称加密算法的要求。例如我们在使用压缩软件给我们的文档数据进行加密的时候,我们输入的密码一般也就十位左右。当我们传入的密钥长度没有达到要求时,这些算法在处理我们传入的key时,会使用PBE(Password Based Encryption)把Key和一些随机数杂糅后计算出真正的密钥。
非对称加密算法
在上面的对称加密算法中,我们可以看到,由于加密和解密使用的Key是相同的,所以这让暴力破解成为了可能。而且Key的传输和保存也是一个大问题。那么非对称加密算法就出现了。
非对称式密码学也称之为 公开密钥密码学(Public-key cryptography)。是密码学的一种算法,它和对称加密算法最大的不同就是它加密使用一个密钥,解密使用另外一个密钥。我们把用于给文件加密使用的密钥称之为公钥。而我们用于解密的密钥称之为私钥。
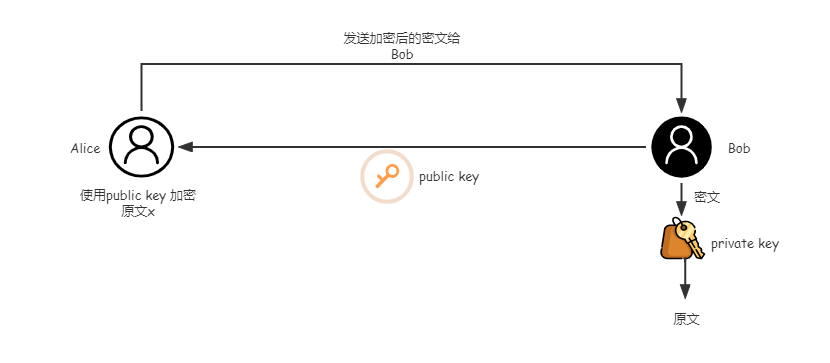
加密与解密过程
- Alice 现在需要透过不安全的互联网向 Bob 发送信息。
- Alice 撰写好原文——
之后,由于没有加密,所以不能发出。 - Bob使用密码学安全伪随机数生成器产生一对密钥,其中一个作为公钥为
,另一个作为私钥 。 - Bob可以通过任何方法把公钥
给Alice。不用担心公钥被泄密。 - Alice用得到的公钥
加密自己的原文 ,得到密文 。 - Alice把密文
通过任何方法发送给Bob。 - Bob收到密文,用私钥
对密文进行解密 ,得到Alice撰写的明文 - 即使公钥和密文都被窃听了,但是由于没有私钥,还是不能对密文进行解密。
Diffie-Hellman Key exchange
非对称加密算法可以追溯到1976年的Diffie-Hellman Key exchange。这个是一种可以在双方没有任何预先信息的条件下通过不安全的信道传输非密钥的数据而建立起双方同时使用的一个密钥,并用此密钥来实现对称加密的方法。这样就避免了密钥直接在不安全的网络中传输的过程。
它的具体过程如下:
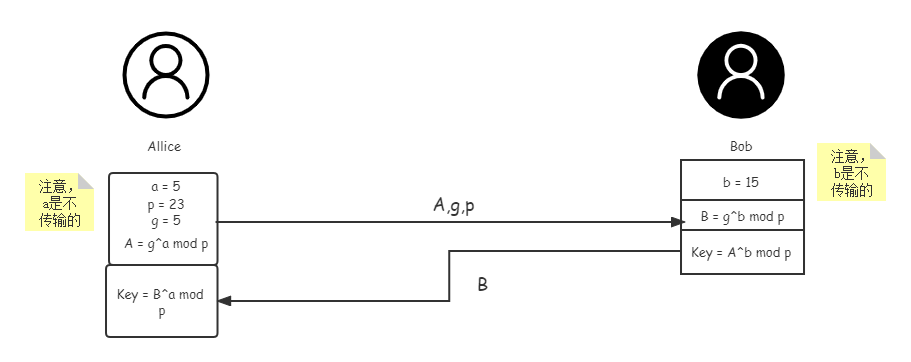
我们可以看到,Alice :
非对称算法的具体实现-RSA算法
1977年,三位数学家Rivest、Shamir 和 Adleman 设计了一种算法,可以实现非对称加密。这种算法用他们三个人的名字命名,叫做RSA算法。从那时直到现在,RSA算法一直是最广为使用的”非对称加密算法”。毫不夸张地说,只要有计算机网络的地方,就有RSA算法。这种算法非常可靠,密钥越长,它就越难破解。根据已经披露的文献,目前被破解的最长RSA密钥是232个十进制位,也就是768个二进制位,因此可以认为,1024位的RSA密钥基本安全,2048位的密钥极其安全。
RSA算法原理
首先需要先了解一点基础的数论知识:
- 素数(质数):大于1的自然数中,只能被自己和1整除的数。
- 互质:N个整数的最大公因子是1,则称这N个整数互质。
- 同余:当两个整数除以同一个正整数,得到了相同余数,则这两个正整数同余。
欧拉函数
给定正整数n,在小于等于n的正整数之中,有多少个与n构成互质关系的数?
欧拉函数
- 如果n是质数的某一个次方,即 n = p^k (p为质数,k为大于等于1的整数),则φ(n) = φ(p^k) = p^k - p^(k-1)。也就是φ(8) = φ(2^3) =2^3 - 2^2 = 8 -4 = 4
- 如果n是质数,则 φ(n)=n-1 。因为质数与小于它的每一个数,都构成互质关系。比如5与1、2、3、4都构成互质关系。
- 如果n可以分解成两个互质的整数之积,即 n = p * k ,则φ(n) = φ(p * k) = φ(p1)*φ(p2)。例如φ(56) = φ(8) * φ(7) = 4 * 6 = 24
欧拉定理
如果两个正整数
也就是说,
模反元素
如果两个正整数
也就是说,
$${ed }\ \equiv\ {kx}+1\qquad \qquad \qquad [3]$$
那么
当我们再对欧拉定理进行一下变形:
我们把
我们使用这种方法来进行加密和解密,即m 的 e乘上d 次方为加密运算,得到结果 c,c 模以 n 为解密运算,得到结果 m。这似乎可以用于加密和解密。但这样,加密的结果会非常大。明文数据将非常小。
当我们再回顾之前所提到的Diffie-Hellman Key exchange。之前提到
我们可以看到,当我们把
非对称算法的应用
其实非对称算法不仅仅只有RSA算法,但是其他算法的核心思想也和RSA算法大同小异。所以我们在这里就不再谈论其他算法了。RSA算法也是大量应用在日常互联网的生活中。例如HTTPS网页的访问、PGP加密软件的使用等。
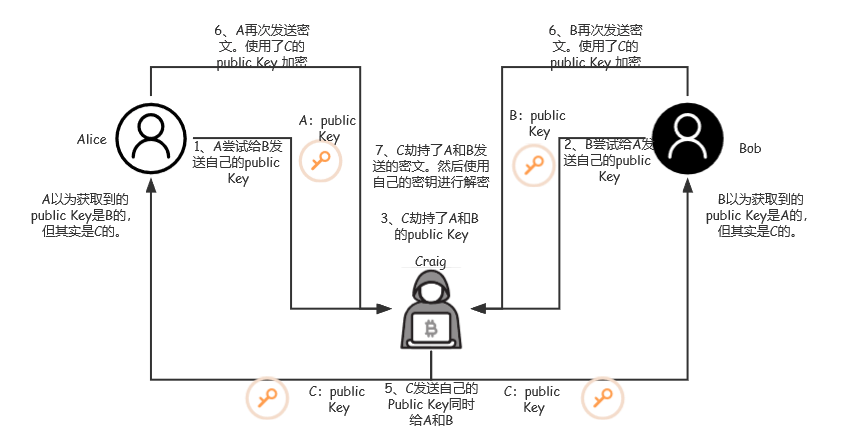
非对称加密的安全隐患
在说SSL之前,我们还需要看一下非对称加密的不足性。在一切的最开始,由于A,B不是单方面的通信,所以A和B要通过网络交换public key。如果C在中间拦截了呢?假设有这种情况,C拦截了A和B的public key,又分别用自己的public key发给A和B。A和B并不知道,他们还以为这个public key来自对方。当A给B发消息时,A先用自己的private key加密数据的hash值,之后用C传来的假的public key加密数据,再发出去。C拦截到之后,先用C自己的private key解密数据,C就获取了A的原始信息!之后,C可以篡改数据内容,再用自己的private key加密数据的hash值,用之前拦截的B的public key加密数据,再发给B。B收到以后,先用自己的private key解密数据,再用C传来的假public key解密hash值,发现匹配。这样,B收到了一条来自C的假的信息,但是B还以为信息来自于A。中间人攻击仍然可能存在
CA
这个时候,我们就需要CA(Certificate Authority)这个机构的存在了。他们的作用就是保证public Key 的真实性。CA也是基于非对称加密算法来工作。有了CA,B会先把自己的public key(和一些其他信息)交给CA。CA用自己的private key加密这些数据,加密完的数据称为B的数字证书。(使用private Key 加密也称之为签名。因为加密之后,内容如果在传输途中被拦截并使用其public Key解密。则由于劫持方没有你的private Key,他不能再把原文进行加密。从而达到确认传输的内容没有被修改的目的)现在B要向A传递public key,B传递的是CA加密之后的数字证书。A收到以后,会通过CA发布的CA证书(包含了CA的public key),来解密B的数字证书,从而获得B的public key。CA把自己的CA证书集成在了浏览器和操作系统里面。A拿到浏览器或者操作系统的时候,已经有了CA证书,没有必要通过网络获取,那自然也不存在劫持的问题。
现在A和B都有了CA认证的数字证书。在交换public key的阶段,直接交换彼此的数字证书就行。而中间人C,还是可以拦截A和B的public key,也可以用CA证书解密获得A和B的public key。但是,C没有办法伪造public key了。因为C不在CA体系里面,C没有CA的private key,所以C是没有办法伪造出一个可以通过CA认证的数字证书。如果不能通过CA认证,A和B自然也不会相信这个伪造的证书。所以,采用CA认证以后,A和B的public key的真实性得到了保证,A和B可以通过网络交换public key(实际是被CA加密之后的数字证书)。
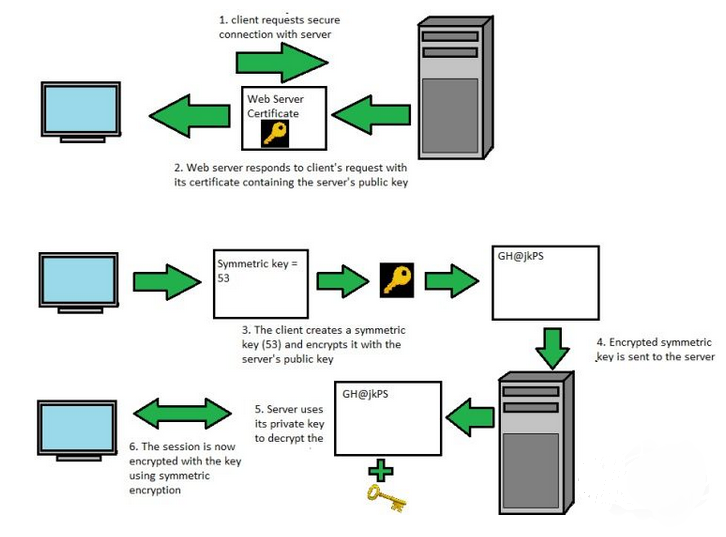
SSL
现在我们每天访问的大量网站中,基本都是HTTPS(Hyper Text Transfer Protocol Secure)网页,以前,我们的网页都是HTTP(Hyper Text Transfer Protocol)。这个传输协议是不安全的。传输的过程中,各种信息都有可能被泄露。而HTTPS网页就是使用的SSL(Secure Socket Layer)或者TLS(Transport Layer Security)(后者比较新,但我们一般使用SSL统称这两个)。
其具体流程如下:
- 通过CA体系交换public key
- 通过非对称加密算法(例如RSA算法)交换用于对称加密的密钥
- 通过对称加密算法,加密正常的网络通信
非对称加密算法比对称加密算法要复杂的多,处理起来也要慢得多。如果所有的网络数据都用非对称加密算法来加密,那效率会很低。所以在实际中,非对称加密只会用来传递一条信息,那就是用于对称加密的密钥。当用于对称加密的密钥确定了,A和B还是通过对称加密算法进行网络通信。这样,既保证了网络通信的安全性,又不影响效率。